2300 words
There are numerous misconceptions about evolution. One of the largest, in my opinion, is that there is some sort of intrinsic ‘progress’ to evolution. This is inferred from the fact that the first life—bacteria—are simpler and less ‘complex’ than so-called ‘higher’ organisms. This notion is still pushed by some, despite the fact that it is a discredited concept.
The concept of scala naturae was first proposed by Aristotle (Hodos, 2009; Werth, 2012; Diogo, Ziermann, and Linde-Medina, 2014). This notion was held until Darwin’s landmark book On the Origin of Species (Darwin, 1859) when Darwin proposed the theory of evolution by natural selection. However, the notion of the scala naturae is still entrenched in modern-day thought, from the layman all the way to educated scientists. This notion is wrong.
Neuroscientist Herculano-Houzel writes on page 94 of her book The Human Advantage A New Understanding of How Our Brain Became Remarkable:
Moreover, evolution is not synonmous with progress, but simply change over time. And humans aren’t even the youngest, most recently evolved species. For example, more than 500 new species of cichlid fish in Lake Victoria, the youngest of the great African Lakes, have appeared since it filled with water some 14,500 years ago.
When people think of ‘progression up this evolutionary tree’ they look at Man as the ultimate culmination of the evolutionary process—as if every event that occurred before the Dawn of Man was setting the stage for us to be here. This, of course, goes back to the scala naturae concept. The ‘lower’ animals are the ones that are less ‘complex’ than the ‘higher’ animals. The notion that there was a ‘march of progress’ towards Man is erroneous (see Gould, 1989: 27-45 for a review).
Indeed, even Darwin himself didn’t believe in some ‘straight line’ to the evolutionary process. In one of his notebooks, he drew a ‘coral of life’ (seen below):

Notice how there are no ‘lower’ or ‘higher’ organisms and each branch branches off to the side, with no way of denoting which organism has ‘progressed’ more?
The scala naturae proposes that inanimate objects, to plants, to animals can all be placed somewhere on this ladder of ‘progress’, which eventually culminate with Man at the top—as if we are the ultimate culmination of evolutionary history and time—like we were preordained to be here. The scala naturae is still with us today. Why should we view humans as ‘higher than’ other organisms? It doesn’t make sense. It’s clearly steeped in a large anthropometric bias.
Indeed, the scala naturae is so entrenched in our minds that modern-day biologists still use terms that would denote ‘higher’ and ‘lower’, the scala naturae. Rigato and Minelli (2013) data mined 67,413 biological articles published between the years 2005 and 2010 looking for signs of pre-evolutionary language (e.g., lower vs. higher vertebrates and lower vs. higher plants). Of the 67,413 article that were mined for data, 1,287 (1.91%) returned positive hits for scala naturae language. Shockingly, the journal Molecular Biology and Evolution had frequent scala naturae language (6.14 %) along with the journal Bioessays (5.6%) and the Annual Review of Ecology, Evolution, and Systematics (4.82%). Clearly, misconceptions about the nature of evolution can still persist in the modern-day amongst experts (that doesn’t mean that the notion of the scala naturae is correct since specialists still use some of the terminology, however). In terms of scala naturae thinking by country, Russia topped the list followed by Japan, Germany, Israel, and France.
This notion of ‘progress’ to evolution—that there is some sort of scala naturae with has ‘primitive’ organisms on the bottom with ‘advanced’ organisms at the top is wrong. When comparing organisms, the comparison isn’t between which organism is more ‘primitive’ or ‘advanced’. The comparison is between ancestral and derived, so the only meaningful comparison is to say that organism A is more like the common ancestor (ancestral) while organism B has derived traits in comparison to the common ancestor (Gregory, 2008).
It is further assumed that earlier organisms are more ‘primitive’ than organisms that are younger. This is false. Once organisms diverge from a common ancestor, they both share a mixture of ancestral and derived traits; ancestral and derived organisms share a mix of ancestral and derived traits from said common ancestor (Crisp and Cook, 2005: 122). Furthermore, ‘early’ does not denote ‘primitiveness’ (Gould, 1997: 36). So to say that, for instance, ‘this organism on this tree did less/no branching than others and is therefore primitive’ is incorrect. It is fallacious to make a comparison between ‘primitive’ and ‘advanced’ organisms. For instance, one may look at a phylogeny and see a straight line and assume that no change has occurred. This is wrong.
The terminology ‘driven’ and ‘passive’ is used to denote trends in complexity. Is the trend driven or passive? Large amounts of research has been done into this matter (Gould, 1996; McShea, 1996) with no clear-cut answer. What is increasing? Complexity? The thing about ‘complexity’ (whatever that is) is that it may be a trend, but it is not an inevitability (Werth, 2012: 2135). Since life began at the left wall—where no organism can get any simpler—there was only one way to go: up. Any organism that arises in between the left and right walls can either become more or less complex depending on what is needed in that particular ecosystem.
Gould (1996) speaks of a drunkard leaving a bar. The drunkard leans on the bar wall (the left wall of complexity) and continuously stumbles toward the gutter (the right wall of complexity). The drunkard may go back and forth, touching the bar wall all the while getting closer to the gutter which each stumble. The drunkard will—eventually—end up in the gutter. Now we can look at the right wall of complexity as us humans and the left wall as bacteria. Any organism caught in the middle of the walls can either get less or more complex, but no simpler than the left wall—where life began. Some may say that this denotes ‘progress’, however, since life began constrained at the left wall, there was no way to go but ‘up’.
McShea (1994: 1761) notes:
If such a trend in primates exists and it is driven, that is, if the trend is a direct result of concerted forces acting on most lineages across the intelligence spectrum, then the inference is justified. But if it is passive, that is, forces act only on lineages at the low-intelligence end, then most lineages will have no increasing tendency. In that case, most primate species—especially those out on the right tail of the distribution like ours—would be just as likely to lose intelligence as to gain it in subsequent evolution (if they change at all).
Are there any instances like this in our genus? Of course there are, with the most famous (and most studied) being Homo floresiensis. I’ve written twice before about how the evolution of floresiensis proves that 1) evolution is not progress and 2) large brains need high-quality energy and without that brain size—and body size—will shrink. Indeed, a new paper on the evolution of floresiensis lends credence to the idea that floresiensis is a derived form of erectus (Diniz-Filho and Raia, 2017). Their analysis lends credence to the support that floresiensis is derived from erectus and not habilis. No matter which hominin floresiensis evolved from, this shows how critical the quality of energy is for maintaining a large brain and body size and, without large amounts of high-quality energy then reductions in brain and body size will persist. This, yet again, lends more credence to my argument of non-progressive evolution.
Now, I must talk about the scala naturae and its involvement in attempting to figure out the evolution of the human brain. Does the supposed increase in brain size denote ‘progress’ in evolution? No, it does not.
Brains are made from metabolically expensive tissue; that is, the larger a brain is the more kcal are needed to power it. Brains and the tissue that compose it (along with other bodily structures) are so expensive that there is a trade-off between elaborate defense mechanisms and brain size—as EQ decreases, defense mechanisms get more elaborate and vice-versa (Stankowich and Romero, 2017). So organisms don’t need intelligence—and [sometimes] the larger brain that comes with it—if they have evolved elaborate defense mechanisms to where they don’t need a large brain to survive.
The increase in brain size over the past few million years in our genus Homo is pointed at as proof that evolution is ‘progressive’, however that is literally only one metric and any wild swings in environment can and will select for smaller brains. The point is that increases in brain size are due to local change, so therefore trends in the opposite direction can and do occur.
The terms ‘higher and lower’ in regards to the scala naturae have been discredited (Diogo, Ziermann, and Linde-Medina, 2014: 18). Indeed, when we believe that things may go our way when, say, we are testing ourselves compared to other animals we will invoke the scala naturae. But what if we humans are not the ‘best’ at any given task tested? Eleven animal species (including human infants) were tested to analyze color processing speed. First came honeybees, then fish, then birds and lastly human infants. Of course this contradicted the scala naturae concept, and some people even argued that learning speed is not a useful measure of intelligence (Chittka et al, 2012)! This scala naturae thinking would have us believe that we should be on top of the learning speed ‘pyramid’, yet when it’s found that we are not then we say that learning speed is not a useful measure of intelligence? Can you see the huge bias there?
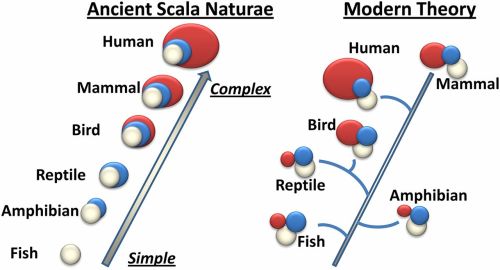
Above is a figure from Mashour and Alkire (2013) which shows the evolution of the brain through the lens of the scala naturae concept on the left and the modern theory on the right. Clearly, with the modern theory, there is no such ‘progress’ or ‘inherent advancement’ from fish culminating to the brain of Man.
Modern theories of the scala naturae include John Bonner’s assertion that animals found in lower strat are ‘lower’ whereas those found in the higher strata are ‘higher’. This erroneous assumption made by Bonner, however, is corrected in subsequent publications (see Randomness in Evolution, Bonner, 2013). He stresses, as can be seen by the title of the book, that evolution is random and possibly non-drive (i.e., passive, see McShea, 1994, Gould, 1996) (Diogo, Ziermann, and Linde-Medina, 2014: 3). Furthermore, there is “no general trend to increase the number of muscles at the nodes leading to hominoids and to modern humans. That is, with respect to the muscles in the regions we have investigated, although modern humans accumulated more evolutionary transitions than the other primates included in our cladistic study, these evolutionary transitions did not result in more muscles, or more muscle components (Diogo & Wood, 2011, 2012a,b; Diogo et al., 2013b)” (Diogo, Ziermann, and Linde-Medina, 2014: 18). So looking at this one facet of hominin evolution (muscles), there is no general increase in the number of muscles at the nodes leading to our genus.
Next, one Dale Russel (who I have written about at length) needs to be addressed again. Russel asserts that had the dinosaurs not gone extinct, that one species of dinosaur, the troodon, would have evolved human-like bipedalism, a large brain among other traits. This is horribly incorrect. In his book (Russel, 1989) he denotes ever-increasing complexity, which, as I have noted, is due to the beginnings of life at the left wall of complexity. The behaviors of most dinosaurs which were inferred from skeletal morphology and trackways “may not have lain much outside the observed range in ectothermic crocodilians” (Hopson, 1977: 444), along with most dinosaur endocasts showing not showing a tendency for increased brain size (Hopson, 1977: 443). Further, since dinosaurs were tied to the sun their behavior was restricted, they needed to avoid getting too hot or cold and couldn’t explore and understand the world, and in turn wouldn’t have been able to evolve large brains—nevermind human-like intelligence (Skoyles and Sagan, 2002: 12). Russell’s contentions are moot.
On that same note, E.O. Wilson, author of the 1975 book Sociobiology asserts that evolution must be progressive (I will cover Wilson’s views on evolutionary progress in depth in the future) since life started prokaryotes with no nucleus, to eukaryotes with nucleus and mitochondria, then multi-cellular organisms with complex organs like eyes and brains and finally the emergence of the human mind (Rushton, 1997: 293). This, too, can be explained by life beginning at the left wall and having nowhere to go ‘but up’.
This finally brings me to JP Rushton who attempted to revive the scala naturae concept by (wrongfully) applying r/K selection theory to human races. Rushton argues that since Mongoloids are the ‘newest’ race that they are then the most ‘progressed’ and thusly are a pinnacle of evolution of Man. However, as anyone who understands evolution knows, evolution through natural selection is local change, not progress.
This notion of evolutionary progress, the scala naturae, and the ‘march up the evolutionary tree’ are all large misconceptions about the nature of evolution. This misconception arises due to only looking at the right tail of the variation. Of course, if you only looked at the right tail, you would assume that evolution is ‘progressive’, that there was a ‘march’ from simple to complex organisms. Why focus only on the complex end of the distribution of life? Because looking at the whole of life, bacteria is the mode (Gould, 1996; 1997). We are currently living in the age of the bacteria. That is the mode of all life, and that is why there is no ‘progress’ to evolution, nor any ‘march up an evolutionary tree’, because evolution through natural selection is local change, not progress.
Saying that evolution is progress doesn’t allow us to appreciate the full house of variation (Gould, 1996). Bacteria rule the earth, and will do so until the Sun explodes. What does that tell you about any ‘progress’ to life? Aboslutely nothing because bacteria have remained the most numerous lifeforms on the planet since life began.
More Rocks exist that bacteria.
Rocks dominate bacteria at existing because more exist.
But even if rocks dominate, Humans build computers.
Complexity may increase at random but I see it as more of a sorting algorithm.
Such as how high IQ people associate more with high IQ people today.
Mate selection and environmental complexity increased intelligence.
High IQ people gravitate to complex jobs and other places.
Rocks may be superabundant organisms but a segment of humans is increasing in complexity well rock are not (accept the rocks humans turn into computers)
If you do not think rock are organisms just look at cave crystals and stalagmites and stalactites.
LikeLike
No, they are not organisms. Just because they can accumulate and form shapes, they have no reason to synthesize or capture energy, necessitate Carbon, or even have the basic requirement of DNA.
LikeLike
Does not matter if rocks are not organisms. The point is the complexity scale. If you want to go to the lowest scale we get to rock. The point of Race Realist saying bacteria dominate is because they are the least complex organism but the most mass. And if we go by that metric rocks dominate bacteria because more rocks exist that bacteria and they are less complex than bacteria. He used to bacteria analogy to show Humans are not dominant on earth because more bacteria exist that humans. So I made an even more ridiculous claim that rocks are more dominate than bacteria and humans because more rock exists then either. I believe humans are dominated even if more bacteria exist. Bacteria are actually more dominant than rocks in that respect also even though more rocks exist.
LikeLike
“Does not matter if rocks are not organisms. The point is the complexity scale. If you want to go to the lowest scale we get to rock. The point of Race Realist saying bacteria dominate is because they are the least complex organism but the most mass. And if we go by that metric rocks dominate bacteria because more rocks exist that bacteria and they are less complex than bacteria. He used to bacteria analogy to show Humans are not dominant on earth because more bacteria exist that humans. So I made an even more ridiculous claim that rocks are more dominate than bacteria and humans because more rock exists then either. I believe humans are dominated even if more bacteria exist. Bacteria are actually more dominant than rocks in that respect also even though more rocks exist.”
Yet it DOES matter because you make the assumption that the criteria for “dominance, by evolutionary complexity, applies to all matter.
Rocks lack the essence of Organisms to actually make them relevant in comparisons. They are an aspect of the environment, a resource, but not an organism.
It’s an apples and oranges comparison.
LikeLike
But Yet supposed they did qualify, they would indeed dominate. They have no need for water, they do have the most mass in the universe compared to organisms, and whatever mass extinction comes it’s way, Rocks will survive.
So it takes a little bit more critical thinking than just say “ridiculous” to actually scientific legitimize “dominance”.
LikeLike
OK forget rocks.
Why should bacteria be said to be dominant rather than humans?
Just because more exist?
Does it not count what humans have done?
Art, philosophy, technology.
I think intelligence should qualify us as dominant.
What achievements have bacteria achieved that they are superior?
LikeLike
“Does it not count what humans have done?
Art, philosophy, technology.
I think intelligence should qualify us as dominant.”
Art and Philosophy can be simple narrowed down, in terms of evolutionary significance, to guiding cultures which in turn influence genetics which doesn’t necessarily mean better “adaptation” or fitness.
Technology basically given us better lifespan and more focus on mental processes, but also resulted in Weaker bodies (dysgenic result of agriculture) and modern issues in terms of resource reliance based on our modern needs in electricity and otherwise.
So Intelligence does have it’s advantages, in evolutionary context it also has it’s trade offs.
Also, you are aware that Bacteria also adapted WITH US and aid in our digestion, a vital function?
LikeLike
Yes, I know bacteria are part of us.
But what is the reasoning behind RaceRealist last statements that bacteria are better than us.
Humans can write science papers on bacteria.
Bacteria cannot write papers on us.
LikeLike
Humans can use science to understand the brain.
A dog cannot even know what the scientific method is.
There is a reason humans rule the planet and not dogs.
LikeLike
“Saying that evolution is progress doesn’t allow us to appreciate the full house of variation (Gould, 1996). Bacteria rule the earth, and will do so until the Sun explodes. What does that tell you about any ‘progress’ to life? Aboslutely nothing because bacteria have remained the most numerous lifeforms on the planet since life began.”
Clear as day. He doesn’t say they are “higher” or better, he says that simply they have always been the most numerous and their versatility aids theme in various adaption scenarios.
“Humans can write science papers on bacteria.
Bacteria cannot write papers on us.”
And in a evolutionary significance…this means what? Us relying on them for energy needs does however imply an important development.
LikeLike
AK, bacteria are biological organisms, rocks are not.
Yes, I wouldn’t say ‘dominate’ though. They are the most numerous bioligcal organism on the planet, have been since the inception of life and will be until all life on earth ends.
I see where you’re coming from, but bacteria are bio organisms, rocks are inanimate objects. You’re, ironically, using scala naturae thinking saying that rocks are ‘below’ bacteria.
Because bacteria are more numerous. The argument is that we look at the right tail end of ‘complexity’ and assume that, by looking at a small amount of organisms at the right end, that there is some sort of ‘drive’ to become more complex. But the drunard’s walk scenario by Gould puts that to rest.
I never made this claim, if I did please quote the part so I can remove it.
The point is that bacteria are more numerous then we, they are the mode of all life.
LikeLike
“Humans can use science to understand the brain.
A dog cannot even know what the scientific method is.
There is a reason humans rule the planet and not dogs.”
Eh, human use various resources for their own means for the sake of their survival to increase lifespan, which I’ve mentioned before will backfire.
Dogs are a DOMESTICATED RESULT that were designed to adapt to human lifestyles, thus are not a direct product of nature for apt comparison.
LikeLike
RR,
Humans can understand the world.
We are conscious of knowing we exist.
The complexity of a brain usually makes it more intelligent.
Complex brain migrate to complex environments.
As civilization advances in complexity with a segment of humans adapt to this complexity?
Humanity is complexifying.
LikeLiked by 1 person
“Humans can understand the world.
We are conscious of knowing we exist.
The complexity of a brain usually makes it more intelligent.
Complex brain migrate to complex environments.
As civilization advances in complexity with a segment of humans adapt to this complexity?
Humanity is complexifying.”
To put this in more comprehensible prose, complex neural systems, such as ours, create our own environments and overtime the became more complex.
Yet at the same time we became more dependent on our synthesized resources that they backfire outside more merely us using limited resources.
For instance, human communication
http://www.huffingtonpost.com/suren-ramasubbu/does-technology-impact-a-childs-emotional-intelligence_b_7090968.html
We’ve managed to “control” our environments to give optimal lifespans, but that doesn’t necessarily reflect long term versatility against nature without some sort of dependency, one of various ones being an actual fraction of the population that actually makes this happen.
Bacteria need none of it.
LikeLike
“Bacteria need none of it.”
As a choice being human is better to me than being a bacteria.
The reason is that I like thinking and I would rather be a thinker than a slime mold. It is fun using my intelligence. I really would not be happy having a lifespan of 12 days.
Some people like the Amish reject technology. I grew up in it so I cannot let it go. I would be unhappy being Amish.
LikeLike
“As a choice being human is better to me than being a bacteria.
The reason is that I like thinking and I would rather be a thinker than a slime mold. It is fun using my intelligence. I really would not be happy having a lifespan of 12 days.”
Being happy and being invested in thinking is basically another development of human psychology involved in it’s neural logical maintenance as a social animal.
Irrelevant in the overall significance of reproduction and survival of a species in a objective sense, but in a human context it’s meaningful.
“Some people like the Amish reject technology. I grew up in it so I cannot let it go. I would be unhappy being Amish.”
And others could feel opposite as well, feeling happier away from materialism, narcissism, and lack of values and solidarity that would characterize more “modern” culture.
I’m not judging which is right, but both are mainly human relevant in of themselves.
LikeLike
And rocks even exist on other planets, lol.
LikeLike